Buscando la máxima concordancia entre particiones: un problema abierto

Para la primera contribución invitada de este blog, tenemos la gran suerte de contar con una entrada escrita por José Enrique Chacón. José Enrique es profesor titular de Estadística en el Departamento de Matemáticas de la Universidad de Extremadura, miembro del Instituto de Matemáticas de esa universidad y también miembro del equipo de investigación de nuestro proyecto. Ha publicado numerosos artículos en diversos problemas estadísticos, entre los que se pueden mencionar la estimación no paramétrica de funciones de densidad y el análisis de clústeres.

En su entrada nos habla de algunas sutilezas que aparecen cuando uno trata de medir el grado en el que están de acuerdo dos expertos cuando abordan un problema de clasificación. Al final de la entrada y como reza el título, se plantea una cuestión relacionada con este asunto que lleva abierta bastantes años, por si a alguien le gustan los retos complicados…

Buscando la máxima concordancia entre particiones: un problema abierto

Es habitual encontrarnos con la situación genérica en la que se han usado dos metodologías distintas para etiquetar una serie de objetos, siendo nuestro propósito comparar las dos particiones resultantes.

Cuando las etiquetas corresponden a categorías prefijadas, con un significado concreto, estamos ante un problema de clasificación. En cambio, cuando las etiquetas se utilizan para revelar la existencia de ciertos subgrupos homogéneos, a priori ocultos dentro de un todo, entonces estamos hablando de análisis clúster.

Clasificación

Por ejemplo, podríamos pensar en dos expertos en diagnóstico que, trabajando separadamente, clasifican a un grupo de pacientes en las categorías de enfermo y sano. Cada experto proporcionará una clasificación (posiblemente distinta, pero similar) de esos pacientes, y nos gustaría cuantificar el grado de concordancia entre ambos expertos.

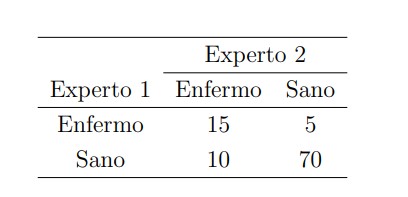
El primer paso a la hora de realizar dicha comparación consiste en construir lo que se llama una tabla de contingencia, que recoge el número de objetos en común de cada posible pareja de categorías. En nuestro ejemplo, esto se traduce en una tabla $2\times 2$ que registra cuántos pacientes han sido clasificados como enfermos por ambos expertos, o como enfermos por el primer experto pero sanos según el segundo, o viceversa, o cuántos han sido etiquetados como sanos por ambos expertos. Más gráficamente, podríamos tener una tabla como ésta:

De los 100 pacientes del ejemplo, los expertos han coincidido en el diagnóstico de 15+70=85 de ellos, con lo que la proporción de concordancia observada sería $p_o=85/100=0.85$ . El mayor grado de concordancia se da, lógicamente, cuando la tabla de contingencia es diagonal, en cuyo caso tendríamos $p_o=1$ .

Dicha proporción observada parece ser un buen indicador del grado de acuerdo entre ambos expertos. Sin embargo, si realizamos el sencillo experimento de asignar etiquetas al azar en los dos expertos, puede sorprendernos que la proporción de concordancia resultante no es cercana a 0, sino que está en torno a 0.5. Esto ocurre porque hay un cierto grado de concordancia $p_e$ debido puramente al azar.

Para tener en cuenta este fenómeno, la propuesta habitual es corregir la proporción de concordancia mediante la fórmula

$\kappa=\frac{p_o-p_e}{1-p_e}.$

Este nuevo coeficiente, llamado kappa de Cohen, simplemente sustrae de la concordancia observada la esperada por el azar y luego normaliza para que siga valiendo 1 en el caso de concordancia perfecta. Así, un valor $\kappa\simeq0$ indica un grado de concordancia parecido al que se hubiera obtenido al asignar las etiquetas al azar. Aunque la kappa de Cohen no está exenta de críticas, es usada frecuentemente en muchos ámbitos, especialmente en psicología.

En el cálculo de $p_e$ , lógicamente, influye el modelo de aleatoriedad considerado para la tabla de contingencia. Lo habitual no es asignar las etiquetas completamente al azar, como habíamos sugerido antes, sino fijando las marginales de la tabla para hacer dicho cálculo. Es decir, en nuestro ejemplo, para calcular $p_e$ cogeríamos etiquetas al azar, pero manteniendo que el experto 1 tiene una proporción $20/80$ entre enfermos y sanos, y análogamente con un $25/75$ para el experto 2. Esto reduce el número de grados de libertad a 1, porque conociendo una de las entradas de la tabla $2\times 2$ ya quedan totalmente determinadas todas las demás. Así, como en el caso del test exacto de Fisher, dicha entrada libre tiene distribución hipergeométrica y se obtiene que

$p_e=p_{11}p_{12}+p_{21}p_{22},$

donde $p_{ij}$ es la proporción de objetos que el método $i$ asigna a la categoría $j$ . En el ejemplo de los expertos, $p_e=\frac{20}{100}\cdot\frac{25}{100}+\frac{80}{100}\cdot\frac{75}{100}=0.65$ . Con esto, tendremos $\kappa\simeq0.57$ , lo que rebaja la percepción inicial sobre el alto grado de concordancia de los dos expertos.

Análisis clúster

Imaginemos ahora que tenemos una serie de pacientes diagnosticados con una cierta enfermedad, y que se sospecha que entre esos casos podría haber varios subtipos de esa enfermedad. En base a ciertos análisis de los pacientes, un experto podría inferir que existen dos subgrupos distintos de personas que presentan características similares entre sí, y así concluir que en realidad los resultados ocultaban dos variantes de la enfermedad, dando lugar a una partición de los pacientes en dos grupos $C_1$ y $C_2$ . Y otro experto, trabajando con una metodología diferente, podría agrupar a esos mismos pacientes en dos categorías distintas $D_1$ y $D_2$ .

Llegaríamos entonces a construir una tabla de contingencia como la del ejemplo anterior, pero a la hora de comparar ambas particiones habría que tener en cuenta ciertas peculiaridades de esta nueva situación, que la hacen diferente del escenario previo. Sin ir más lejos, una distribución como ésta

significaría una total falta de acuerdo en el problema de clasificación, pues no contiene ningún elemento en la diagonal. Y, sin embargo, en el contexto de análisis cluster dicha tabla se corresponde con un acuerdo total entre los expertos, ya que los subgrupos que se han formado son exactamente los mismos, sólo que el primer experto ha llamado grupo 1 a los elementos que el segundo experto ha etiquetado como grupo 2, y viceversa. Esto ocurre porque a priori no existían categorías prefijadas dentro del conjunto de pacientes estudiado, sino que se han descubierto mediante su análisis.

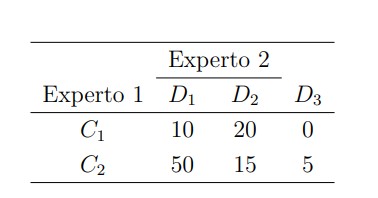
Más aún, podría ocurrir que la metodología empleada por el segundo experto distinguiera 3 variantes de la enfermedad, en lugar de 2, en cuyo caso la tabla de contingencia sería de tipo $2\times 3$ , como por ejemplo

Aquí, mientras que el experto 1 sigue distinguiendo un primer grupo con 30 individuos y un segundo con 70, el experto 2 ha agrupado en una primera categoría a 60 pacientes (la mayoría de ellos, correspondientes al segundo grupo del experto 1), en una segunda categoría a 35 de ellos, y ha revelado un posible tercer grupo con 5 miembros.

En esta situación, para comparar los resultados es habitual estudiar la disposición de parejas de observaciones en ambas particiones, de modo que, sean cuales sean las dimensiones de la tabla de contingencia, sólo es necesario considerar 4 posibles situaciones: las parejas de objetos que están asignadas a un mismo grupo, en las dos particiones; o las que están en el mismo grupo en la primera partición, pero en grupos distintos en la segunda partición; o viceversa; o las parejas que están en distintos grupos en ambas particiones. Podemos llamar $a$ , $b$ , $c$ , $d$ , respectivamente, al número de parejas en cada una de esas 4 situaciones. El grado de concordancia se mide, entonces, mediante la proporción de parejas que tienen la misma disposición en ambas particiones, es decir, utilizando

${\rm RI}=\frac{a+d}{a+b+c+d},$

que se conoce como índice de Rand. En el ejemplo anterior, $a=\binom{10}{2}+\binom{50}{2}+\binom{20}{2}+\binom{15}{2}+\binom{5}{2}=1575$ , porque podemos formar $\binom{10}{2}$ parejas distintas en las que sus dos miembros están en un mismo grupo para el experto 1 (el grupo $C_1$ ) y también están en un mismo grupo para el experto 2 (el grupo $D_1$ ), etc. Análogamente, $d=1300$ y $a+b+c+d=\binom{100}{2}$ , de modo que ${\rm RI}=2875/4950\simeq0.58$ .

Pues bien, igual que ocurría con la proporción de concordancia en clasificación, resulta que el índice de Rand también registra cierto grado de acuerdo que se debe puramente al azar. Para corregir esta deficiencia se emplea el índice de Rand ajustado, definido como

${\rm ARI}=\frac{{\rm RI}-\mathbb E[{\rm RI}]}{1-\mathbb E[{\rm RI}]},$

donde $\mathbb E[{\rm RI}]$ se refiere al valor esperado del índice de Rand, cuando las entradas de la tabla de contingencia se eligen al azar, pero respetando las distribuciones marginales (igual que en el caso de la kappa de Cohen). El cálculo de esta esperanza, basado en una distribución hipergeométrica generalizada, se detalla en un artículo muy citado de Hubert y Arabie (1985).

Y en ese mismo artículo se plantea el problema, aún abierto, al que alude el título de esta entrada. ¿Cuál es la máxima concordancia posible, ya sea medida con el ${\rm RI}$ o con el ${\rm ARI}$ , cuando se fijan las marginales de las particiones comparadas? Diversos algoritmos se han propuesto para resolver el problema numéricamente, pero hasta ahora sólo el caso $2\times2$ ha sido resuelto de forma explícita, en una publicación reciente del autor de esta entrada (Chacón, 2021). Así que, desde aquí, se anima a cualquier avispado lector a que estudie este problema, que acumula ya más de 35 años desde su planteamiento sin una respuesta para el caso general.

Referencias

Chacón, J.E. (2021). Explicit agreement extremes for a $2\times2$ table with given marginals. Journal of Classification, 38, 257-263. preprint | doi
Hubert, L. and Arabie, P. (1985). Comparing partitions. Journal of Classification, 2, 193-218.

Buscando la máxima concordancia entre particiones: un problema abierto

Buscando la máxima concordancia entre particiones: un problema abierto

Referencias

Publicado por JRB

Un comentario sobre “Buscando la máxima concordancia entre particiones: un problema abierto”

Deja un comentario Cancelar la respuesta

Buscando la máxima concordancia entre particiones: un problema abierto

Referencias

Comparte esta entrada:

Relacionado

Publicado por JRB

Un comentario sobre “Buscando la máxima concordancia entre particiones: un problema abierto”

Deja un comentario Cancelar la respuesta